Vocabularry Part Of Body and Shape

English Vocabulary

The Human Body and Anatomy

Useful Vocabulary

The Human Body

ankle | arm | chest | foot | hand | knee leg | neck | shoulder	back | bottom | calf | elbow | head heel | thigh
Close up on the foot	Close up on the hand
ankle | big toe | heel | little toe | toenail	index finger | knuckle | fingernails little finger | middle finger ring finger | thumb | wrist

Build Up

Inside the Body - Simple Anatomy

bladder	The organ inside the body of a person, where urine is stored before it leaves the body.
bone	The hard parts inside a human or animal that make up its frame.
brain	The organ inside the head that controls thought, memory, feelings and activity.
digestive system	The organs in your body that digest food.
ear	The ear is made up of three different sections: the outer ear, the middle ear, and the inner ear. These parts all work together so you can hear and process sounds.
eye	'The eyes takes in information about the world around you - shapes, colours, movement, and more. Then they send the information to your brain.
heart	The heart sends blood around the body. The blood provides oxygen and nutrients to the body.
kidney	One of the main jobs of the kidneys is to filter the waste out of the blood.
liver	A large organ in the body which cleans the blood and produces bile (a bitter yellow liquid which helps to digest fat).
lungs	The lungs are one of the largest organs in the body, they work with the respiratory system to take in fresh air, and get rid of stale air.
mouth	The opening in the face which consists of the lips and the space between them, or the space behind which contains the teeth and the tongue.
skeleton	The frame of bones that support the body.
spine	The line of bones down the centre of the back that provides support for the body.
teeth	The hard white objects in the mouth, which are used for biting and chewing.
tooth	(see above)
urinary tract	The parts of the body which produce and carry urine.

Naturally Speaking

Describing aches and pains

If your head hurts:	"I've got a headache." or "My head aches."
If your stomach hurts:	"I've got stomach ache." or "My stomach aches."
If your back hurts:	"I've got backache." or "My back aches."
If your neck hurts:	"I've got neckache." or ""My neck aches."
If other parts of your body hurt:	"I've got a pain in my arm / leg etc."

Dialogue

Listening Practise:- It's Monday morning and Mr Smith has gone to see the doctor.
Doctor:	Hello Mr Smith. We haven't seen you in a while. What seems to be the problem?
Mr Smith	Well, I fell off the ladder whilst I was decorating and hurt my ankle. It swelled up and hasn't gone down since.
Doctor:	OK - let's have a look, take off your shoe and sock and roll up your trouser leg. (Examines ankle) Ah yes, I think we had better send you to the hospital to get this X-rayed. You may have broken a bone.
Mr Smith:	What? You're joking! No wonder it hurts so much.

 

 

 

S H A P E S

Shape

This article is about describing the shape of an object. For common shapes, see list of geometric shapes. For other uses, see Shape (disambiguation).

The shape (Old English: gesceap, created thing) of an object located in some space is a geometrical description of the part of that space occupied by the object, as determined by its external boundary – abstracting from location and orientation in space, size, and other properties such as colour, content, and material composition.

Mathematician and statistician David George Kendall writes:^[1]

In this paper ‘shape’ is used in the vulgar sense, and means what one would normally expect it to mean. [...] We here define ‘shape’ informally as ‘all the geometrical information that remains when location, scale^[2] and rotational effects are filtered out from an object.’

Simple shapes can be described by basic geometry objects such as a set of two or more points, a line, a curve, a plane, a plane figure (e.g. square or circle), or a solid figure (e.g. cube or sphere). Most shapes occurring in the physical world are complex. Some, such as plant structures and coastlines, may be so arbitrary as to defy traditional mathematical description – in which case they may be analyzed by differential geometry, or as fractals.

Contents

Rigid shape definition

In geometry, two subsets of a Euclidean space have the same shape if one can be transformed to the other by a combination of translations, rotations (together also called rigid transformations), and uniform scalings. In other words, the shape of a set of points is all the geometrical information that is invariant to translations, rotations, and size changes. Having the same shape is an equivalence relation, and accordingly a precise mathematical definition of the notion of shape can be given as being an equivalence class of subsets of a Euclidean space having the same shape.

Shapes of physical objects are equal if the subsets of space these objects occupy satisfy the definition above. In particular, the shape does not depend on the size and placement in space of the object. For instance, a "p" and a "d" have the same shape, as they can be perfectly superimposed if the "p" is translated to the right by a given distance, rotated upside down and magnified by a given factor (see Procrustes superimposition for details). However, a mirror image could be called a different shape. For instance, a "b" and a "d" have a different shape, at least when they are constrained to move within a two-dimensional space like the page on which they are written. Even though they have the same size, there's no way to perfectly superimpose them by traslating and rotating them along the page. Similarly, within a three-dimensional space, a right hand and a left hand have a different shape, even if they are the mirror images of each other. Shapes may change if the object is scaled non uniformly. For example, a sphere becomes an ellipsoid when scaled differently in the vertical and horizontal directions. In other words, preserving axes of symmetry (if they exist) is important for preserving shapes. Also, shape is determined by only the outer boundary of an object. For example, a solid ice cube and a second ice cube containing an inner cavity (air bubble) have the same shape.

Objects that can be transformed into each other by rigid transformations and mirroring are congruent. An object is therefore congruent to its mirror image (even if it is not symmetric), but not to a scaled version. Objects that have the same shape or one has the same shape as the other's mirror image (or both if they are themselves symmetric) are called geometrically similar. Thus congruent objects are always geometrically similar, but geometrical similarity additionally allows uniform scaling.

Non-rigid shape definition

A more flexible definition of shape takes into consideration the fact that realistic shapes are often deformable, e.g. a person in different postures, a tree bending in the wind or a hand with different finger positions. By allowing also isometric (or near-isometric) deformations like bending, the intrinsic geometry of the object will stay the same, while sub-parts might be located at very different positions in space. This definition uses the fact that, geodesics (curves measured along the surface of the object) stay the same, independent of the isometric embedding. This means that the distance from a finger to a toe of a person measured along the body is always the same, independent of posture. By only considering geodesic distances or other isometric properties as done in spectral shape analysis, it is possible to retrieve all cats in a database of animals independent of the pose.

Colloquial shape definition 

Shape can also be more loosely defined as "the appearance of something, especially its outline". This definition is consistent with the above, in that the shape of a set does not depend on its position, size or orientation. However, it does not always imply an exact mathematical transformation. For example it is common to talk of star-shaped objects even though the number of points of the star is not defined.

Philosophical skepticism of definitions

In Plato's Meno, Socrates questions Meno as to the most accurate definition of a figure/shape. By showing the possibility of there being more than one definition, Socrates shows that a definition cannot wholly and accurately describe something and that there is no one absolute definition for anything including shape.^[3]

Shape analysis

Main article: Statistical shape analysis

The modern definition of shape^{[clarification needed]} has arisen in the field of statistical shape analysis. In particular Procrustes analysis, which is a technique for analyzing the statistical distributions of shapes. These techniques have been used to examine the alignments of random points. Other methods are designed to work with non-rigid (bendable) objects, e.g. for posture independent shape retrieval (see for example Spectral shape analysis).

Shapes is all the geometrical information that remains when location, scale and rotational effects are filltered out from an object

And this is some of them..


 

 

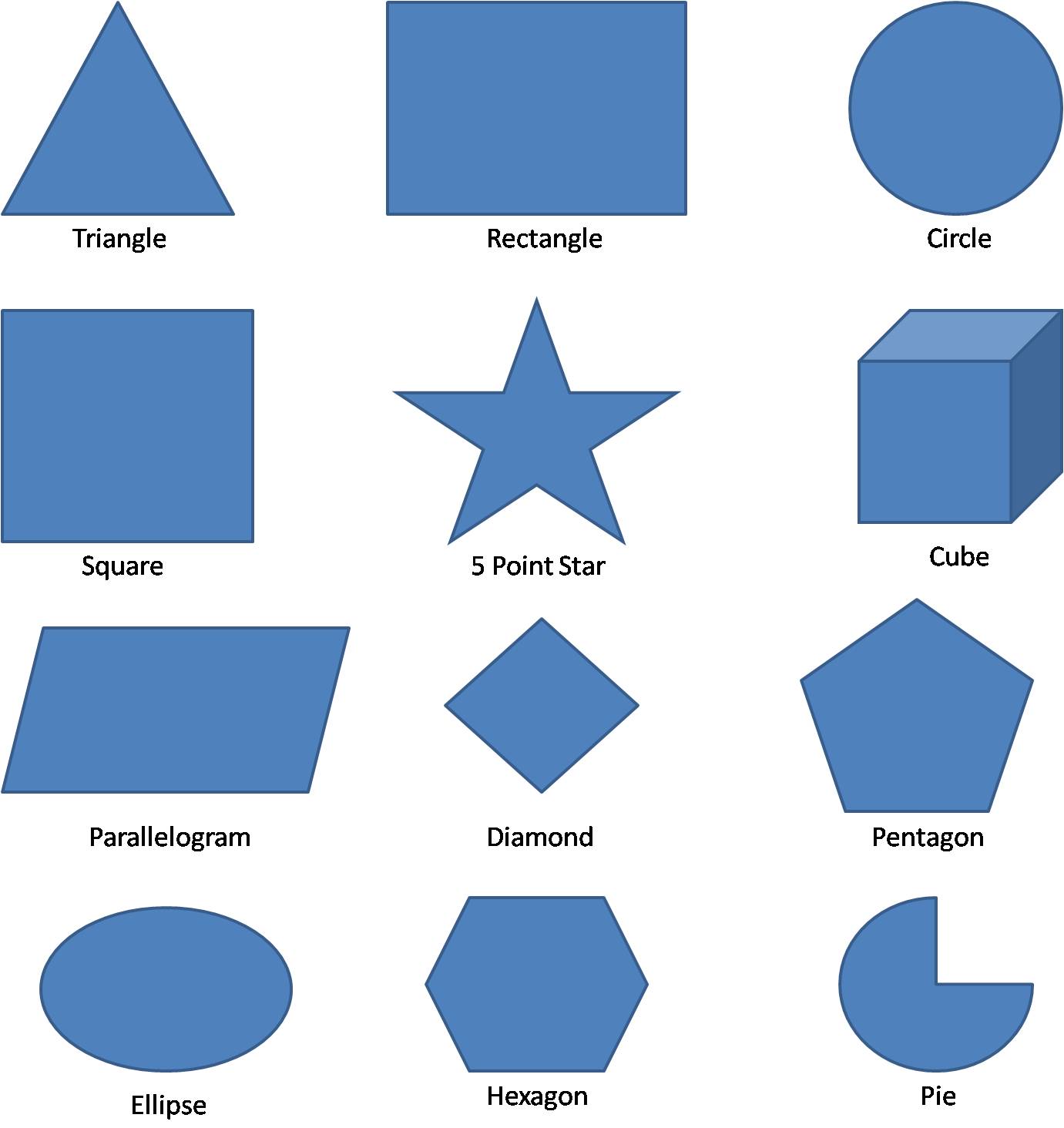
Triangle

 

  Circle

 

Hexagon

 

 Parallelogram

 

 Octagon

 

Oval

 

Pentagon

 

Rectangle

 

Square

 

                                                 Trapezium

PETAL



HEART














SHEL